Ruutvõrrandi ax² + bx + c = 0 diskriminant on
- Summa a + b + c
- Ruutvõrrandi lahendite korrutis
- Avaldis b² - 4ac
- Avaldis
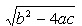
- Avaldis b² + 4ac
Ruutvõrrandil ax² + bx + c = 0, kus a ei ole null
- on kaks lahendit, kui diskriminant pole negatiivne
- on kaks lahendit, kui diskriminant on positiivne
- on kaks lahendit, kui diskriminant on negatiivne
- on alati 2 reaalarvulist lahendit
- pole kunagi lahendeid
Võrrandil x² + 2x + 2005 = 0 pole reaalarvulisi lahendeid, sest
- lineaarliikme x kordaja on paaritu arv
- vabaliige on positiivne
- võrrandi diskriminant on negatiivne
- võrrandi diskriminant on positiivne
- kõik kordajad on positiivsed
Võrrandil -7x² = 0
- on lõpmata palju lahendeid
- on kaks võrdset lahendit (mõlemad on nullid)
- on kaks erinevat lahendit
- pole ühtegi lahendit
- on üks lahend (see on 0)
Missugused väited on tõesed (3 õiget)?
Võrrandi
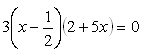 lahendid on
lahendid on- -0,4 ja 0,5
- -0,4 ja -0,5
- 0,4 ja 0,5
- 0,4 ja -0,5
- Mõni muu vastus
Võrrandi –(x – 6)(x – 1) = 6
- lahendid on 4 ja 3
- lahendid on 4 ja (–3)
- lahendihulk on tühi hulk
- lahendid on (–4) ja 3
- lahendid on 0, 3 ja 4
Ruutvõrrandi graafiline lahendamine tähendab seda, et
- joonestatakse parabool ning leitakse graafiku ja x-telje lõikepunktide x koordinaadid
- joonestatakse parabool ning leitakse graafiku ja y-telje lõikepunktide x koordinaat
- kontrollitakse, kas parabool avaneb allapoole või ülespoole
- joonestatakse parabool ja leitakse graafiku ja y-telje lõikepunkti y koordinaat
- joonestatakse parabool ning leitakse graafiku ja x-telje lõikepunktide y koordinaadid
Ruutfunktsioonile y = ax² + bx + c (a < 0) vastaval ruutvõrrandil pole lahendeid. Kuidas paikneb see parabool teljestikus?
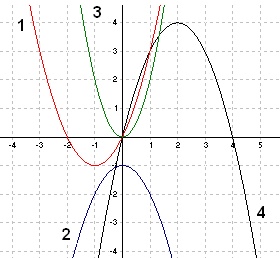
- Nii nagu joon 1
- Nii nagu joon 2
- Nii nagu joon 3
- Nii nagu joon 4
- Mõni muu variant
Võrrandi x² = –16
- lahendiks sobib iga arv
- lahendid on 4 ja (–4)
- lahend on 0
- lahendid puuduvad
- lahend on 4
Võrrandi –(–x – 5)² = 0
- lahendiks on arv 0
- lahendiks on iga (–5)-st suurem arv
- lahendiks on iga (–5)-st väiksem arv
- lahendiks on (–5) (kahekordne lahend)
- lahendihulk on tühi hulk (arvu ruut ei saa null olla)
Adalbärt pidi lahendama võrrandi –x² – 4x + 5 = 0 Viete´i valemite abil. Missugusel juhul toimis ta õigesti?
- Et p = –4 ja q = 5, siis püüdis leida arve, kus lahendite korrutis on 5 ja summa 4. Kuna selliseid arve pole, siis pole võrrandil lahendeid
- Et p = –4 ja q = 5, siis püüdis leida arve, kus lahendite korrutis on 5 ja summa 4.
- Korrutas võrrandi mõlemad pooled (–1)-ga ning üritas leida arve, mille korrutis on (–5) ja summa (-4)
- Korrutas võrrandi mõlemad pooled (–1)-ga ning üritas leida arve, mille korrutis on (–5) ja summa 4
Võrrandi x(x – 3) = x lahendamisel jagas Juku võrduse mõlemad pooled x-ga ja sai lahendiks x = 4. Mida arvad?
- Juku tegi valesti, tundmatuga ei tohi jagada, lahendid võivad kaotsi minna
- Juku tegi kõik õigesti
- Juku tegi valesti, sest x = 4 pole selle võrrandi lahend
- Juku oleks pidanud kõigepealt sulud avama, koondama ja siis lahendivalemit kasutama
- Ei oska kohe midagi arvata
Valemi
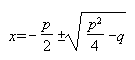 abil lahendatakse
abil lahendatakse- lineaarvõrrandit
- taandamata ruutvõrrandit
- taandatud ruutvõrrandit
- mittetäielikku ruutvõrrandit
- ruutvõrrandit, mille kordajad ja vabaliige on täisarvud
Võrrandi (2x – 3)(5x + 2) = 0 lahendamiseks
- proovin järjest arve (–100)-st 100-ni
- kasutan korrutise nulliga võrdumise tingimust, s.t. lahenditeks
sobivad x = 1,5 ja x = –0,4 - proovin järjest arve (–10)-st 10-ni
- avan sulud, koondan sarnased liikmed ja lahendivalemi abil leian lahendid
- joonestan funktsiooni y = (2x - 3)(5x + 2) graafiku, leian parabooli ja x-telje
lõikepunktide x-koordinaadid. See on kõige täpsem lahendusviis
Võrrandi 2005x² = 0
- lahendiks ei sobi ükski arv
- lahendiks sobib vaid arv 2005
- lahendiks sobivad kõik positiivsed arvud
- lahendiks sobib vaid arv 0
- lahendiks sobib iga arv
Juku pidi graafiliselt lahendama võrrandid 1) x² – 5x + 4 = 0; 2) x² – 4x = 0 ja 3) –x² + 3,5x + 2 = 0. Selleks joonestas ta vastavad paraboolid. Kuidas saab Juku teada, kas nendel võrranditel on ühine lahend.
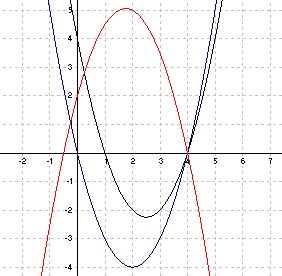
- ühise lahendi korral lõikuvad paraboolid x-teljel ühes ja samas punktis
- ühise lahendi korral lõikuvad paraboolid y-teljel ühes ja samas punktis
- Juku lahendab kõik võrrandid valemi abil ja uurib siis lahendeid
- Juku teeb iga funktsiooni kohta tabeli –3-st 3-ni ja püüab sealt ühiseid lahendeid leida
Võrrandil 2x² = 18
- on üks lahend, see on 0
- on kaks lahendit (–9 ja 9)
- pole lahendeid, sest ühegi arvu ruut pole 18
- on kaks lahendit (–3) ja 3
- on üks lahend, x = 3
Võrrandi ax² + bx + c = 0 lahendamiseks kasutatakse valemit
- x = a : b
- x = –b : a
-
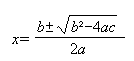
-
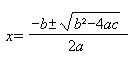
- x = a + b + c
Kuidas lahendatakse võrrand (x²)² – 2x² – 3 = 0?
- Asendusvõttega, tähistatakse t = x² ja edasi lahendatakse ruutvõrrand t² - 2t - 3 = 0.
Esialgsel võrrandil võib olla 4 lahendit - Proovimise teel
- Seda võrrandit ei saagi lahendada
- Tehakse asendus x = t
- Asendusvõttega, tähistatakse t = x² ja edasi lahendatakse ruutvõrrand t² - 2t - 3 = 0.
Juku pidi graafiliselt lahendama võrrandi 0,5x² – 3x – 1 = 0. Selleks tegi ta joonise ja kirjutas lahenditeks x = –0,31662 ja x = 6,31662. Mida arvad selliselt lahendusest?
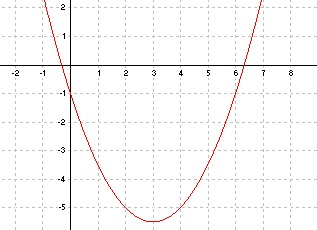
- Juku ei saa anda sellise täpsusega lahendeid
- Juku oli erakordselt tubli
- Juku tegi vale joonise
- Juku lahendus oleks õige, kui võrdusmärgi asemel oleks ligikaudse võrduse märgid
- Juku oleks pidanud lahendid ümardama kahe kohaga peale koma