Leia igale küsimusele kõige täpsem vastus
© Allar Veelmaa, Tiigrihüppe Sihtasutus ja Loo Keskkool 2005

1. Lihtsusta avaldis
   

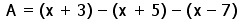
   1.   ?    –x + 5
   2.   ?    x + 5
   3.   ?    –x – 5
   4.   ?    –x + 12
   5.   ?    –x – 12

2. Lihtsusta avaldis
   

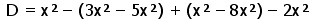
   1.   ?    –2x²
   2.   ?    2x²
   3.   ?    –16x²
   4.   ?    –12x²
   5.   ?    –14x²

3. Hulkliikmete 3x + 2y – 1 ja 3x – 2y + 1 summa on

   1.   ?    6x
   2.   ?    4y
   3.   ?    2
   4.   ?    6x + 4y + 2
   5.   ?    6x – 4y – 2

4. Missugune järgmistest hulkliikmetest on kolmliige?

   1. 3x + 2y + 1
   2. –3x – 4y + 3z + 1
   3. 3x
   4. x + y – x
   5. 1 + 2 + 3
   Kontrolli!

5. Kolmekohalises naturaalarvus on x sajalist, y kümnelist ja z ühelist. Selle arvu üldkuju on

   1.   ?    x + y+ z
   2.   ?    100x · 10y · z
   3.   ?    xyz
   4.   ?    100x + 10y + z
   5.   ?    x – y – z

6. Lihtsusta avaldis
   

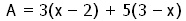
   1.   ?    –2x + 9
   2.   ?    –2x – 9
   3.   ?    –8x + 9
   4.   ?    8x + 9

7. Hulkliikmete x + y + 3z ja 1 + 2z + x + y summa on

   1.   ?    2x + 2y + 5z + 1
   2.   ?    2x + 2y + 5z
   3.   ?    –1 + z
   4.   ?    1 – z
   5.   ?    x + 3yz + 4zx

8. Millega võrdub (x + y + z)²?

   1.   ?    x² + y² + z² + 2xy + 2xz + 2yz
   2.   ?    x² + y² + z² – xy – xz – yz
   3.   ?    x² + y² + z²
   4.   ?    x² + y² + z² + xy + xz + yz
   5.   ?    x² + y² + z² – 2xy – 2xz – 2yz

9. On teada, et hulkliikmed 3x² + 5x + 12 ja Ax² – Bx + 12 on võrdsed. Millega võrduvad A ja B?
   

   1.   ?    A = 3 ja B = –5
   2.   ?    A = 3 ja B = 5
   3.   ?    A = 5 ja B = 3
   4.   ?    A = 5 ja B = –3

10. Hulkliikme –4x + 6y jagamisel 2-ga saame tulemuseks

    1.   ?    –4x + 6y
    2.   ?    –2x – 3y
    3.   ?    –2x + 3y
    4.   ?    2x + 6y

11. Kolmnurga küljed on a, b ja c. Hulkliikme a + b + c abil leiame

    1.   ?    pool kolmnurga ümbermõõdust
    2.   ?    kahekordse kolmnurga pindala
    3.   ?    kolmnurga pindala
    4.   ?    teravnurkde arvu
    5.   ?    kolmnurga ümbermõõdu

12. Kahekohalises arvus on a kümnelist ja b ühelist. Selle arvu üldkuju on

    1.   ?    a + b
    2.   ?    10a + b
    3.   ?    ab
    4.   ?    10x + y
    5.   ?    10b + a

13. Kuidas avaldub joonisel oleva värvitud kujundi pindala?
    
    

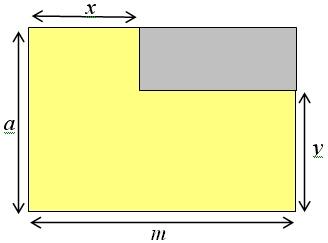
    1.   ?    am – (m – x)(a –y)
    2.   ?    am + (m – x)(a – y)
    3.   ?    am – (m + x)(a – y)
    4.   ?    am – (m – x)(a + y)

14. On teada, et võrdus kehtib. Missugune avaldis peab olema sulgudes, kui
    –7xy + 14y = 7y (..............)

    1.   ?    –x + 2
    2.   ?    x – 2
    3.   ?    x + 2
    4.   ?    –x – 2
    5.   ?    Mõni muu vastus

15. Mis on hulkliikmes J ühine tegur, mille saab lihtsustamisel sulgude ette võtta?
    
    

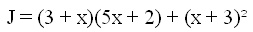
    1.   ?    x + 3
    2.   ?    (x + 3)²
    3.   ?    5x + 2
    4.   ?    (x + 3)(5x + 2)
    5.   ?    (x + 3)²(5x + 2)
    6.   ?    Mõni muu vastus

16. Millega võrdub hulkliikme 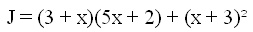väärtus, kui x = –1?

    1.   ?    –2
    2.   ?    –9
    3.   ?    7
    4.   ?    9
    5.   ?    Mõni muu vastus

17. Kuidas avaldub hulkliikmena joonisel oleva kollase vaiba ümbermõõt?
    

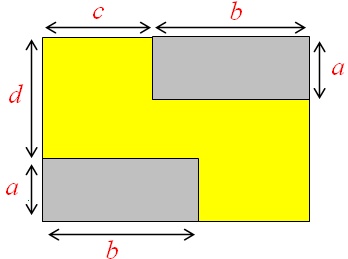
    1.   ?    2a + b + 2c + 2d
    2.   ?    a + b + c + d
    3.   ?    2( a + b + c + d)
    4.   ?    Seda ei saa nende andmete korral arvutada
    5.   ?    a + 2b + 2c + 2d
    6.   ?    2a + 2b + c + 2d
    7.   ?    2a + 2b + 2c + d

18. Risttahuka põhiservad on pikkusega x ja x² ja kõrgus on x. Kuidas avaldub risttahuka täispindala?

    1.   ?    
    2.   ?    
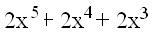
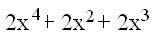
    3.   ?    2x³ + 2x² + 2x
    4.   ?    x³
    5.   ?    x · x² · x
    6.   ?    4x³ + 2x²

19. Missugusel juhul avatakse sulud õigesti?
    –4a(2x – 3y + z – 1)

    1.   ?    –8ax + 12ay – 4az + 4a
    2.   ?    –8ax + 12ay – 4az – 4a
    3.   ?    8ax + 12ay – 4az + 4a
    4.   ?    –8ax – 12ay – 4az + 4a
    5.   ?    Mõni muu vastus

20. Leia jagatis (2x³ – 8x² – 4) : (–4)

    1.   ?    –0,5x³ + 2x² + 1
    2.   ?    0,5x³ + 2x² + 1
    3.   ?    –0,5x³ – 2x² + 1
    4.   ?    –0,5x³ + 2x² – 1
    5.   ?    –0,5x³ + 2x²

21. Leia korrutis 0,5(–2x – 4y + 6z + 8)

    1.   ?    –x – 2y + 3z + 4
    2.   ?    –x – 2y + 3z
    3.   ?    –x + 2y + 3z + 4
    4.   ?    x – 2y + 3z + 4
    5.   ?    Mõni muu vastus